Wednesday, October 31, 2007
Homework due tomorrow
No homework. Enjoy your trick-or-treating!
ELA:
Study your WWWs
Write a paragraph using your WWWs. Keep parts of speech in mind.
Tuesday, October 30, 2007
Homework due tomorrow
Workbook pages 45 and 46
ELA:
Write a 2-page essay about the worst or best Halloween experience you have had
Write sentences using WWWs
Announcements:
Get you progress reports signed
Monday, October 29, 2007
Homework due tomorrow/WWW quiz correction directions
Do your test corrections in the correct format (you can look through the blog, as I posted the information you need for preparing good test corrections)
ELA:
Write WWWs 10X and find definitions of the words
Do WWW quiz corrections:
Word Wall Word Test Correction Directions
1) Answer the same 6 reflection questions you have to answer to do math test/quiz corrections
2)Correct your errors in the fill in the blank section by telling me what you did wrong and how you found the correct answers
3) In the context clues section, re-answer the question and explain what clues you used to select your answer
4) In the making inferences question, elaborate your answers
5) In the parts of speech section, name the correct part of speech for each word and explain why you were confused (Please refer to the post I did on parts of speech to review if you need to)
Word Wall Words #6 and Definitions
Premonition: noun: a feeling of anticipation of or anxiety over a future event
Savage: noun: fierce, ferocious, or cruel; untamed
Survey: verb: to view in detail, esp. to inspect, examine, or appraise formally or officially in order to ascertain condition, value, etc
Hysteric: noun: a person who cannot control his or her outburst of emotion or fear
Opportunities for you: A Better Chance
A Better Chance is the preeminent resource for identifying, recruiting and developing leaders among young people of color in the United States.
Through a unique assessment model, A Better Chance refers academically talented students entering grades 6 through 11 to some of the nation's finest independent and public schools to be considered for placement and financial aid. Students who are successfully placed in one of our 300+ member schools become a part of the signature College Preparatory Schools Program, and receive access to expanded educational and leadership opportunities.
The College Preparatory Schools Program (CPSP) is an academic program that identifies, recruits, places, and supports students of color, in outstanding college preparatory middle and high schools nationally.
At A Better, Chance we recognize that students come from different backgrounds and educational opportunities so each application is evaluated on its own merit. Generally, we select students who:
1) Consistently perform at or above grade level in math and English
2) Have an overall academic average of a B+ or better
3) Are ranked in the top 10 percent of the class
Students are required to take standardized tests. There are no score cut-offs but test scores are used to assess academic strength along with school transcripts, extracurricular activities and personal qualities. Selected applications are sent to our member schools, but it is the admission committees of each member school that make the final admission decisions.
Prospective applicants should get started early; late applications are not encouraged as it severly limits opportunities for placements. Further, our application process begins one year prior to enrolling. For example, if a student is currently in the 8th grade, s/he would be applying for the 9th grade.
For more information: click here: http://www.abetterchance.org/abetterchance.aspx?pgID=866
Opportunities for you: Prep for Prep
Any 7th grader of Black and/ or Latino descent group background who has obtained the scores specified below is eligible to apply for admission to PREP 9. The eligibility criteria to apply to the PREP 9 program are as follows:
Student must have a scaled score of at least 700 on the CTB (or any standardized) Reading test administered during the 2006-2007 school year (6th grade) or student must have a grade point average of 90% and above in major subject areas.
Please be prepared to provide us with a copy of your child’s 2006-2007 Reading scores or a copy of 2006-2007 report card.
Download one of the forms below to learn more about the PREP 9 Admissions process:
Admissions Information (English)
Admissions Information (Spanish)
For more information, please email prep9_admissions@prepforprep.org.
Opportunities for you: TEAK Fellowship
TEAK's application process begins in October each year. Through a comprehensive six-month process, applicants participate in several rounds of screening that include a financial assessment, diagnostic tests, a written application, and interviews. TEAK's five-year Fellowships are awarded based on both academic merit and financial need.
Qualified candidates MUST:
- Be enrolled in the SEVENTH grade at the time of their application
- Attend a PUBLIC or PAROCHIAL school in one of the five boroughs of NYC
- Earn 3s & 4s or 90% AND ABOVE in all grades and on tests
- Come from families WITH FINANCIAL NEED
- Provide proof of academic merit and income
- Be citizens or permanent residents of the United States
Each spring, TEAK accepts 25 students as Fellows. They begin attending the Spring Intensive in May, participate in the Summer Institute following their seventh and eighth grade school years, and begin the High School Placement process by attending after-school and Saturday activities during their eighth grade school year. Fellows enter the Post-Placement program during high school and continue their Fellowship until they go to college.
Saturday, October 27, 2007
Homework due on Monday, 10/29
Those of you who owe me ELA work have to do a 2-page essay for each assignment you missed. That is, if you owe me 10 assignments, then, you must do 10 2-page essays for me. I will be looking at content and grammar. If you put no care of effort into your work, I will be able to see that and will grade accordingly.
You could write about any topic. Some things that you could write about are:
What do you think of 7th grade so far?
What do you like doing on the weekends?
What do you like about our class book, The Outsiders? Why?
Do you feel that you have a voice in society? Why or why not?
What about your neighborhood bothers you? Why?
What makes you proud to be who you are? Why?
What makes you proud to be in the Power Point Class? Why?
What do you want in a teacher? Why?
If you could change anything about your school, what would you change? Why?
If your heart is telling you that you want to write a 20-page story instead of 10 2-page essays, that is fine too. I will not be lenient when grading these, as you should have done your work in the first place.
I am allowing you all to make up work, despite your irresponsibility, because I want you all to go to the high schools of your dreams. Next marking period, I will not allow you to make up any work. You have to learn to be on point and to be responsible. You all are mature and old enough by now.
Love,
Ms. Simmons
Thursday, October 25, 2007
Do your math worksheet
Read your notes on rational and irrational numbers. Know what repeating and a non-repeating decimals are and what terminating and non-terminating decimals are.
ELA:
Study for your WWWs quiz
Study your notes on apostrophes
Study your notes on parts of speech (notes are on this blog!)
Write a 2-page essay on the importance of paying attention in class
Wednesday, October 24, 2007
Repeating/Non-repeating decimals and Terminating and Non-terminating decimals
The word rational refers to something reasonable, understandable, within reason. In short rational numbers are whole numbers, fractions, and decimals - the numbers we CAN understand and that we use in our daily lives.
In mathematical terms a number is rational if you can write it in a form a/b where a and b are integers, b not zero. Clearly all fractions are of that form. Terminating decimal numbers can easily be written in that form: for example 0.67 is 67/100, 3.40938 = 340938/100000 etc.
Terminates means to end. So, if you decimal ends, it is a rational number. For example, .46 is a rational number because it is terminating.
Irrational Numbers:
Rational numbers are contrasted with irrational numbers - such like Pi and square roots of non-perfect squares of numbers. In a sense you can't really understand the irrational numbers, because the name irrational itself means NOT rational, NOT reasonable, NOT understandable, NOT within reasoning powers.
Repeating decimals:
A repeating decimal, also called a recurring decimal, is a number whose decimal representation eventually becomes periodic (i.e., the same sequence of digits repeats indefinitely).
.333333333333... is a repeating decimal because 3 repeats. The (...) tells you that 3 goes on and on and that the decimal is non-terminating, which I will go over shortly. (Look below)
Non-repeating decimals:
Non-repeating decimals are decimals that do not have a repeating pattern. For example, the value for Pi is a non-repeating decimal. Its value is: 3.14159265.... You cannot predict any type of pattern for pi. It's irrational.
Terminating decimals:
Terminating decimals are decimals are decimals that END; they do not go on and on and on and on. 6.5 and 0.0000034 are examples of terminating decimals. They stop. They do not go on and on.
Non-terminating decimals:
Non-terminating decimals do not end. They go on forever. The (...) or the line over your decimals indicated that your decimals are non-terminating.
For example, 6.33333333333.... is non-terminating.
Now, how do we figure out what decimals are rational or irrational?
Irrational decimals will be BOTH non-terminating and non-repeating decimals. All other types of decimals will be rational. That is, if your decimal is not BOTH non-terminating and non-repeating, then, it is not irrational.
For example, if a number is non-terminating, but it is repeating, then it is rational. .3333... is repeating and non-terminating. It is rational because it does not BOTH non-repeating and non-terminating. It satisfies ONLY one of the rules.
Homework due tomorrow
Do worksheet on rational and irrational fractions.
ELA:
Study for your WWW quiz
Study the usage of apostrophes
Study your parts of speech (there is information on the blog about parts of speech)
Write a paragraph using your WWW's
Write a 2-page essay about your favorite character in The Outsiders so far. Please tell me why you selected the character you selected.
Tuesday, October 23, 2007
Homework due tomorrow
Do pages 5 and 6 in your text book
Do your worksheet
ELA:
Do The Outsiders worksheet on Chapter three. Please write reflective responses.
Study for your WWW quiz.
Write sentences for your WWWs.
Word Wall Words #5 and Definitions
Sullenly: adverb: showing irritation or ill humor by a gloomy silence or reserve, ill-humored.
Evade: verb: to avoid or escape by speed, cleverness, trickery
Fiend: noun: a person or thing that causes mischief or annoyance; an evil person
Indignant: adjective: feeling, characterized by, or expressing strong displeasure at something considered unjust, offensive, insulting, or base
Monday, October 22, 2007
Rational and Irrational Numbers
Rational Numbers
A rational number is a number that can be written as a ratio. That means it can be written as a fraction, in which both the numerator (the number on top) and the denominator (the number on the bottom) are whole numbers.
- The number 8 is a rational number because it can be written as the fraction 8/1.
- Likewise, 3/4 is a rational number because it can be written as a fraction.
- Even a big, clunky fraction like 7,324,908/56,003,492 is rational, simply because it can be written as a fraction.
 |
Every whole number is a rational number, because any whole number can be written as a fraction. For example, 4 can be written as 4/1, 65 can be written as 65/1, and 3,867 can be written as 3,867/1.
Irrational Numbers
All numbers that are not rational are considered irrational. An irrational number can be written as a decimal, but not as a fraction.
An irrational number has endless non-repeating digits to the right of the decimal point. Here are some irrational numbers:
π = 3.141592…
= 1.414213…
Although irrational numbers are not often used in daily life, they do exist on the number line. In fact, between 0 and 1 on the number line, there are an infinite number of irrational numbers!
Parts of Speech
For more information besides the many handouts I gave you in class, this site is very helpful. Click here.
Briefly, the noun is a person, place, thing, or idea.
The adjective describes a noun.
The adverb indicates manner, time, place, cause, or degree and answers questions such as "how," "when," "where," "how much". Adverbs generally end in "ly."
The preposition usually indicates the temporal, spatial or logical relationship of its object to the rest of the sentence.
The interjection is a word added to a sentence to convey emotion. It is not grammatically related to any other part of the sentence.
You can use a conjunction to link words, phrases, and clauses, as in the following example:
- I ate the pizza and the pasta.
- Call the movers when you are ready.
he verb is perhaps the most important part of the sentence.
A verb or compound verb asserts something about the subject of the sentence and express actions, events, or states of being.
Word Wall Words #5
Sullenly (adverb)
fiend (noun)
Indignant (adjective)
Evade (verb)
Homework due tomorrow
Do your test corrections for your Unit 2 Test. If you did not get a 100 percent, then, you must do test corrections even if you are satisfied with you grade. There is always room for improvement.
Do workbook pages I put on the board (I'm making sure that you write down the homework in your agenda when I tell you to do so. Thus, you have the pages if you followed directions in class today.)
ELA:
Find the definition of your WWWs
Write the words out 10X each
Study your WWWs just in case you receive a pop quiz.
Do your Review: Parts of Speech packet. (We will go over it in class. I have considered counting it as a quiz card. Take your time.)
Wednesday, October 17, 2007
Homework due tomorrow
**Do your worksheet on scientific notation
**Study for your quiz.
ELA:
**Study for WWW quiz
**Write a paragraph using the WWWs
**In your pronoun packet, read page 118. Read page 119 and do Exercises 1 and 2 on 119 and 120.
**Make 3 predictions about what you think will happen in The Outsiders.
Tuesday, October 16, 2007
Word Wall Words #5 and Definitions
Apprehensive (adjective): uneasy or fearful about something that might happen.
Aloofness (noun): at a distance, esp. in feeling or interest; apart.
Defiance (noun): a daring or bold resistance to authority or to any opposing force.
Contemptuously (adverb): showing or expressing contempt or disdain; scornful.
Scientific Notation Lesson with big numbers
Scientists have developed a shorter method to express very large numbers. This method is called scientific notation. Scientific Notation is based on powers of the base number 10.
The notation is based on powers of base number 10. The general format looks something like this:
N X 10x where N= number greater than or equal to 1 but less than 10 and x=exponent of base 10.
Placing numbers in exponential notation has several advantages.
For very large numbers and extrememly small ones, these numbers can be placed in scientific notation in order to express them in a more concise form.
In addition, numbers placed in this notation can be used in a computation with far greater ease. This last advantage was more practical before the advent of calculators and their abundance.
In scientific fields, scientific notation is still used.
Let's first discuss how we will express a number greater than 10 in such notational form.
Numbers Greater Than 10
We first want to locate the decimal and move it either right or left so that there are only one non-zero digit to its left.
The resulting placement of the decimal will produce the N part of the standard scientific notational expression.
Count the number of places that you had to move the decimal, and that would be your x, exponent.
If it is to the left as it will be for numbers greater than 10, that number of positions will equal x, the exponent, in the general expression above.
As an example, how do we place the number 2340000 in standard scientific notation?
Position the decimal so that there is only one non-zero digit to its left. In this case we end up with 2.34. We know that 2.34 has to be less than 10 and has to be greater than or equal to 1.
Count the number of positions we had to move the decimal to the left and that will be the exponent, x.
So we have: 2.34 X 106 in scientific notation.
That is how we convert from standard form to scientific notation.
Now, how do we go from scientific notation to standard form:
(1) Move decimal point to right the same amount of times your exponent tells you to.
For example, if your base ten exponential has an exponent of 5, you have to move the decimal point to the right 5 times.
That is, 5.67 x 105 is: 567000.
Good luck!! You all did a great job in class today.
Homework due tomorrow, Wednesday, 10/17
Do your worksheet on scientific notation with big numbers
ELA:
Write sentences using your WWWs
Write an 2-page essay about what you think about 7th grade so far. SKIP LINES.
Do your worksheet on conjunctions.
Saturday, October 13, 2007
Homework due on Monday
**Write a 4-page creative story about anything you want. Your story must engage the reader. Remember to use sensory details! SKIP LINES.
Math:
**In your workbook, do pages 27-30.
**Work on your test corrections!!!
Tuesday, October 9, 2007
Word Wall Words #4
Love,
Ms. Simmons
Math Worksheet #3
1. Write the following numbers in exponential form.
5 × 5 × 5 × 5 × 5 × 5 × 5
9 × 9 × 9
7 × 7 × 7 × 10 × 8 × 8
3 × 7 ×7 × 7 × 7 × 3 × 3
1 × 2 × 3 × 3 × 3
2. Write the following numbers as repeated multiplication.
32
43
34
810
3. Evaluate the following expressions:
33 + 32 – (4 + 8)
6 – 9 × (-4)2
31 + 40 + 52
4. Write the squares of the following numbers:
32 = _______
142 = _______
92 = _______
152 = _______
5. Write the square roots of the following perfect squares:
√25 = _______ √36 = _______ √100 = _______ √169 = _______
6. Using the number lines below, show approximately where the value of the square root of the included number is. Be sure to show the whole number before and after the square root.
Show the square root of 11, and the whole numbers that √11 lies between.
Show the square root of 175, and the whole numbers that √175 lies between.
Math Worksheet #2
1. Using the number lines below, give the two whole numbers that each of the following square roots lie between:
√2
√6
√10
√12
√17
√21
√38
√45
√29
2. Without using a number line or a calculator, find the two whole numbers that each of the square roots below lie between:
√80
√110
√200
√175
√215
√115
√99
√70
√150
3. Using a calculator, find the square roots of the following numbers. See if they match what you did in number 2 on the other side of this worksheet.
√80 =
√110 =
√200 =
√175 =
√215 =
√115 =
√99 =
√70 =
√150 =
4. Circle the perfect squares. Then, without using a calculator, give their square root.
169
100
110
60
49
225
5
16
2
5. Write the following numbers in exponential form:
5 × 5 × 5 × 5 × 5 × 5 × 5
6 × 6 × 6
7 × 7 × 7 × 7 × 8 × 8
6. Write the following numbers as repeated multiplication:
72
85
99
52 × 35
Math Worksheet #1
Remember: When multiplying exponentials, there are two laws that can help you simplify the expression.
1st Multiplication Law: If the exponentials have the same base, add the powers.
2nd Multiplication Law: If the exponentials have the same power, multiply the bases.
Use the above laws to simplify the following problems.
1. 123 × 23 = ____________
2. 46 × 36 = ____________
3. 55 × 53 = ____________
4. 254 × 44 = ____________
5. 39 × 339 = ____________
6. 1012 × 104 = ____________
7. 75 × 35 = ____________
8. 246 × 36 = ____________
Problem number 3 follows the 1st law for multiplication of exponentials (bases are the same). Write a problem that follows the 2nd law for multiplication of exponentials and simplify it.
______________________________________________________________________________
______________________________________________________________________________
______________________________________________________________________________
______________________________________________________________________________
Multiplication Laws
Base: The number used as a factor for repeated multiplication (the big number on the bottom)
Power: The number of times the factor is being multiplied, a.k.a. exponent (the number up top)
Simplify: The change to a more simple form (not the same as evaluate or solve!!)
There are laws for simplifying the *multiplication* of exponentials:
1st Multiplication Law: If the exponentials have the same base, the powers can be added: 52 × 53 = 52+3 = 55.
It will be very important for students to see this in proof form, to help them visualize it: 52 × 53 = (5 × 5) × (5 × 5 × 5) = 5 × 5 × 5 × 5 × 5
2nd Multiplication Law: If the exponentials have the same powers, multiply the bases and keep the power: 53 × 63 = (5 × 6)3 = 303
Homework due tomorrow
**3 math worksheets (I will post them online for those of you who were absent)
ELA:
**Write the WWWs ten times each
**Write sentences using the WWWs. Make sure you show me that you know the meaning of the words.
Sunday, October 7, 2007
If you want to get ahead....
Word Wall Words #4
Conclude: (verb) to determine by reasoning; deduce; infer:
Ornery (pg. 39): (adjective) stubborn, having an unpleasant personality
Vaguely (pg. 33): (adverb) not clearly or explicitly stated or expressed
Rebellious (pg. 34): (adjective) defying or resisting some established authority, government, or tradition; insubordinate; inclined to rebel.
Gallant (pg. 37): (adjective) brave, spirited, noble-minded, or chivalrous.
How to do good test corrections?
What’s up with test corrections?
For every test that you take in this class, you are required to do test corrections even if you are satisfied with your grade. The point of test corrections is to give you the opportunity to improve and to demonstrate your understanding of the material.
When are test corrections due?
Test corrections are due a week after your receive your test. That is, if I give you back your test on Tuesday, you must return your test corrections to me by the following Tuesday. Since a week is sufficient time to work on your test correction, any late test corrections will result in a zero.
How to do a good test correction?
1. DO A TEST REFLECTION
On a separate piece of loose-leaf paper (not in your notebook), answer the following questions in complete sentences (so I can understand what you are trying to tell me!).
1. What grade did you get on your test?
2. What grade do you think you deserve (based on how much you learned from this unit)?
3. How much studying did you do for this test? Please describe HOW you prepared for this test.
4. Do you think your studying was effective? Why or why not?
5. Do you think you really UNDERSTAND this material?
2. CORRECT THE QUESTIONS YOU MISSED ON THE TEST ON A SEPARATE PIECE OF PAPER FROM YOUR REFLECTIONS
For EVERY SINGLE QUESTION you missed or lost ANY points on, do ALL of the following:
a. Write out the complete correct answer. (If you missed a multiple-choice question, you must write out an entire complete sentence, not just the letter of the answer. This does NOT mean you have to write out the entire question, just put the question into a complete sentence). You also must SHOW YOUR WORK.
b. You must explain how you came up with the correct answer.
b. Where did you find the correct answer? (This could be your notebook, the textbook, your brilliant teacher, etc)
3. ANSWER THIS LAST QUESTION
6. What (if anything) will you do differently next time while preparing for a test in this class?
4. STAPLE ALL THE PAGES TOGETHER, ATTACH YOUR TEST TO THE BACK, AND TURN THE WHOLE THING IN ON TIME!!!
How much are test corrections worth?
Test corrections are worth a quiz grade. If you do not complete your test corrections, you will get a zero. If your test corrections are late, you will receive a zero. If you received a perfect score on your initial test, then, you get an automatic 100 on the test correction!
Due on Tuesday, October 9
Because of the rapid dismissal, I was unable to give you the homework that I had planned for you. Don't worry. I know how excited you all are for homework. Thus, I will make sure to give you lots of homework when you get back. :)
Enjoy your day off. See you Tuesday.
Wednesday, October 3, 2007
Squares and Square Roots
How to Square A Number
To square a number, just multiply it by itself ...
Example: What is 3 squared?
| 3 Squared | = | 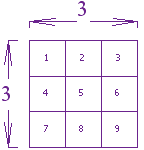 | = | 3 × 3 | = | 9 |
Note: we write down "3 Squared" as 32
(the little "2" means the number appears twice in multiplying)
Some More Squares
| 4 Squared | = | 42 | = | 4 × 4 | = | 16 |
| 5 Squared | = | 52 | = | 5 × 5 | = | 25 |
| 6 Squared | = | 62 | = | 6 × 6 | = | 36 |
Square Root
A square root goes the other direction:
3 squared is 9, so the square root of 9 is 3
| 3 | 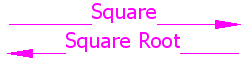 | 9 |
The square root of a number is ...
... that special value that when multiplied by itself gives the original number.
The square root of 9 is ...
... 3, because when 3 is multiplied by itself you get 9.
 | Note: When you see "root" think "I know the tree, but what is the root that produced it?" In this case the tree is "9", and the root is "3". |
Here are some more squares and square roots:
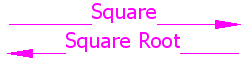 | ||
| 4 | 16 | |
| 5 | 25 | |
| 6 | 36 | |
Example: What is the square root of 25?
Well, we just happen to know that 25 = 5 × 5, so if you multiply 5 by itself (5 × 5) you will get 25.
So the answer is 5
The Square Root Symbol
| This is the special symbol that means "square root", it is sort of like a tick, and actually started hundreds of years ago as a dot with a flick upwards. It is called the radical, and always makes math look important! |
You can use it like this: ![]() (you would say "the square root of 9 equals 3")
(you would say "the square root of 9 equals 3")
More Advanced Topics Follow
You Can Also Square Negative Numbers
Have a look at this:
| If you square 5 you get 25: | 5 × 5 = 25 | |
| But you could also square -5 to get 25: | -5 × -5 = 25 | |
| (because a negative times a negative gives a positive) |
So the square root of 25 can be 5 or -5
There can be a positive or negative answer to a square root!
But when people talk about "the" square root they usually mean just the positive one.
And when you use the radical symbol √ it always means just the positive one.
Example: √36 = 6 (not -6)
Perfect Squares
The perfect squares are the squares of the whole numbers:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | etc | |
| Perfect Squares: | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 | 225 | ... |
It is easy to work out the square root of a perfect square, but it is really hard to work out other square roots.
Example: what is the square root of 10?
Well, 3 × 3 = 9 and 4 × 4 = 16, so we can guess the answer is between 3 and 4.
- Let's try 3.5: 3.5 × 3.5 = 12.25
- Let's try 3.2: 3.2 × 3.2 = 10.24
- Let's try 3.1: 3.1 × 3.1 = 9.61
Very slow ... at this point, I get out my calculator and it says:
3.1622776601683793319988935444327
... but the digits just go on and on, without any pattern. So even the calculator's answer is only an approximation !
(Further reading: these kind of numbers are called surds which are a special type of irrational number)
A Special Method for Calculating a Square Root
There are many ways to calculate a square root, but my favorite method is an easy one which gets more and more accurate depending on how many times you use it:
a) start with a guess (let's guess 4 is the square root of 10)
b) divide by the guess (10/4 = 2.5)
c) add that to the guess (2.5+4=6.5)
d) then divide that result by 2, in other words halve it. (6.5/2 = 3.25)
e) now, set that as the new guess, and start at b) again
... so, our first attempt got us from 4 to 3.25
Going again (b to e) gets us: 3.163
Going again (b to e) gets us: 3.1623
And so, after 3 times around the answer is 3.1623, which is pretty good, because:
3.1623 x 3.1623 = 10.00014
This is fun to try - why not use it to try calculating the square root of 2?Homework due tomorrow
In your workbook, do pages 79 and 80 on square roots.
ELA:
Write a paragraph using your WWW words.
Write a 2-page story about the picture we discussed today. SKIP LINES.
Tuesday, October 2, 2007
Homework due tomorrow
ELA: Write WWW sentences. Make sure your sentences show me that you understand the meanings of the words.
Word Wall Words #3 and Definitions
Roguishly (pg. 22): playfully mischievous (causing annoyance, harm, or trouble)
Incredulous (pg. 24): unbelievable, skeptical
Nonchalantly (pg. 25): coolly unconcerned, indifferent, or unexcited; casual
Feud (pg. 29): a quarrel, fight, or disagreement
Monday, October 1, 2007
Homework due tomorrow
Do your worksheet on exponents
ELA:
Find the definitions of your word wall words.
Write your word wall words 10X.
Study your word wall words.
Announcements:
It seems that we will be taking our exams tomorrow. Make sure you get plenty of rest.
