Wednesday, December 19, 2007
Homework due Thursday, 12/20
ELA: Please write the introductory paragraph to your essay about The Outsiders
Today was a wonderful day! Keep up the great work in class! That's MY PPC!
Love,
Ms. Simmons
Tuesday, December 18, 2007
The Range of a Set of Data
| Problem: | Cheryl took 7 math tests in one marking period. What is the range of her test scores? | ![[IMAGE]](http://www.mathgoodies.com/lessons/vol8/images/testpaper1.gif) |
| 89, 73, 84, 91, 87, 77, 94 | ||
| Solution: | Ordering the test scores from least to greatest, we get: | |
| 73, 77, 84, 87, 89, 91, 94 | ||
| highest - lowest = 94 - 73 = 21 | ||
| Answer: | The range of these test scores is 21 points. | |
| Definition: | The range of a set of data is the difference between the highest and lowest values in the set. | |
In the problem above, the set of data consists of 7 test scores. We ordered the data from least to greatest before finding the range. We recommend that you do this, too. This is especially important with large sets of data.
Homework due Tuesday, December 19
Do a Type 1 writing assignment: Make a list of at least 10 similarities and differences between the movie and the book, The Outsiders.
Math:
Do your worksheet on probability and range
Monday, December 17, 2007
Homework due on Tuesday, December 18
Math: In your math workbook, please do pages 155-158.
Announcements:
I would love to have a holiday celebration with you like we did for Thanksgiving, but lately, you all have been behaving disrespectfully to your other teachers and me. Please show me that you deserve one by being the real Power Point Class.
Sunday, December 16, 2007
Homework due on Monday
ELA: Study for your WWW quiz
You must know:
the spelling and definitions of your WWW's
define a word using context clues
the different types of conflicts in a story
the components of plot
subject/verb agreement
subject/predicate
parts of speech
Wednesday, December 12, 2007
What is setting?
Here are some notes on setting for your reference:
SETTING -- The time and location in which a story takes place is called the setting. For some stories the setting is very important, while for others it is not. There are several aspects of a story's setting to consider when examining how setting contributes to a story (some, or all, may be present in a story):
a) place - geographical location. Where is the action of the story taking place?
b) time - When is the story taking place? (historical period, time of day, year, etc)
c) weather conditions - Is it rainy, sunny, stormy, etc?
d) social conditions - What is the daily life of the character's like? Does the story contain local colour (writing that focuses on the speech, dress, mannerisms, customs, etc. of a particular place)?
e) mood or atmosphere - What feeling is created at the beginning of the story? Is it bright and cheerful or dark and frightening?
Keeping in mind of the setting of a story is important to our understanding of the story. If we know how the setting affects the mood of the story, we gain a better understanding of how the characters in the story are feeling.
Homework due on Thursday, 12/13
Do your test corrections for WWW Quiz 11
Write a paragraph using your WWW's
Write a 3-page essay telling me about your behavior when I was not in class yesterday
If you owe me essays, I hope you are doing your writing. Friday is the last day to hand your make-up work to me!!
Math:
Do your two worksheets on experimental and theoretical probability.
Tuesday, December 11, 2007
Homework due on Wednesday, 12/12
Write sentences using your WWWs
Write a 2-page essay letting me know how your day was since I was not in school to see you today. (SKIP LINES)
Math:
Read over your notes
Announcements:
I already know about your unacceptable behavior today when I was away, and I am very disappointed in you.
Monday, December 10, 2007
Word Wall Words #12
Anxious (adjective)
Enthusiasm (noun)
Reputation (noun)
Distress (noun)
I will not be providing definitions for you online this week because you all need to learn to look into the dictionary and find the definitions yourselves.
Homework due on Tuesday, 12/11
ELA:
Write you word wall words 10X each
Find definitions for your WWW
REMINDER:
If you owe me make-up work, please don't forget to get WRITING!!!
Experimental Probability
Experimental probability of an event is the ratio of the number of times the event occurs to the total number of trials.
Examples of Experimental Probability
Sam rolled a number cube 50 times. A 3 appeared 10 times.
Then the experimental probability of rolling a 3 is 10 out of 50 or 20%.
Solved Example on Experimental Probability
A coin is tossed 60 times. 27 times head appeared. Find the experimental probability of getting heads.
Choices:
A. 1/27
B. 9/20
C. 1/60
D. 3/30
Correct Answer: B
Solution:
Step 1: Experimental probability = number of times the event occurs / total number of trials.
Step 2: Number of times heads appeared = 27.
Step 3: Total number of experiments = 60.
Step 4: So, experimental probability of getting a head = 27/60. Then, you simplify and you get: 9/20.
Sunday, December 9, 2007
Homework due on Monday
Please write all the essays that you owe. You could write about whatever interests you.
Study for your WWW quiz. Look below for information you would need to know on your quiz.
MATH:
No homework.
Thursday, December 6, 2007
Plot and Conflict
Plot Components:
Exposition: the start of the story, the situation before the action starts
Rising Action: the series of conflicts and crisis in the story that lead to the climax
Climax: the turning point, the most intense moment—either mentally or in action
Falling Action: all of the action which follows the climax
Resolution: the conclusion, the tying together of all of the threads
Conflict:
Character vs Character:
This type of conflict finds the main character in conflict with another character, human or not human.
Character vs Nature:
This type of conflict finds the main character in conflict with the forces of nature, which serve as the antagonist.
Character vs Society:
This type of conflict has the main character in conflict with a larger group: a community, society, culture, etc.
Character vs Self:
In this type of conflict, the main character experiences some kind of inner conflict.
Characterization
MAJOR CHARACTERS
They are almost always round or three-dimensional characters. They have good and bad qualities. Their goals, ambitions, and values change. A round character changes as a result of what happens to him or her.
A character who changes inside as a result of what happens to him is referred to in literature as a DYNAMIC character. A dynamic character grows or progresses to a higher level of understanding in the course of the story.
Protagonist: The main character in the story
Antagonist: The character or force that opposes the protagonist.
Foil: A character who provides a contrast to the protagonist.
MINOR CHARACTERS
They are almost always flat or two-dimensional characters. They have only one or two striking qualities. Their predominant quality is not balanced by an opposite quality. They are usually all good or all bad. Such characters can be interesting or amusing in their own right, but they lack depth. Flat characters are sometimes referred to as STATIC characters because they do not change in the course of the story.
POINT OF VIEW: The identity of the narrative voice; the person or entity through whom the reader experiences the story. May be third-person (no narrator; abstract narrative voice, omniscient or limited) or first-person (narrated by a character in the story or a direct observer). Point-of-view is a commonly misused term; it does not refer to the author’s or characters’ feelings, opinions, perspectives, biases, etc.
THESE ARE POINTS OF VIEW:
First Person
The narrator is a character in the story who can reveal only personal thoughts and feelings and what he or she sees and is told by other characters. He can’t tell us thoughts of other characters.
Third-Person Objective
The narrator is an outsider who can report only what he or she sees and hears. This narrator can tell us what is happening, but he can’t tell us the thoughts of the characters.
Third-Person Limited
The narrator is an outsider who sees into the mind of one of the characters.
Omniscient
The narrator is an all-knowing outsider who can enter the minds of more than one of the characters.
Homework due tomorrow
Study for your WWW quiz
On your quiz, you will have to know the meaning of your words and how to spell them correctly.
You will need to know the following:
The four points of view: first person, omniscient, third person limited, and third person objective
The five stages of a story: exposition, rising action, climax, falling action, resolution
Subject/Predicate
Subject/Verb Agreement
Context Clues
Parts of Speech
Math:
Do your math worksheet
Announcement:
Tomorrow, you will be taking a standardized math test. You all will do WELL! Get sufficient rest.
Tuesday, December 4, 2007
Independent and Dependent Events

| There are 3 red candies left in a bag of multicolored candies with a total of 20 candies left in it. The probability that you will get a red one when you reach in is: 3/20. But what are your chances of getting a red one if you reach in again? There are now 19 candies in the bag, and only two are red. The probability is 2/19. Taking the first candy affected the outcome of the next attempt. The two events are dependent. | |
| Now you know that the probability of heads landing up when you flip a coin is 1/2. What is the probability of getting tails if you flip it again? It is still 1/2. The two events do not affect each other. They are independent. | |
Homework due 12/05
Do WWW test corrections
Wrtite sentences using your WWW words
Write a two-page essay where you discuss the following: Why do you come to school each day? What do you get out of coming to school?
Math:
Do your math worksheet
Monday, December 3, 2007
Subject/Verb Agreement
1. When the subject of a sentence is composed of two or more nouns or pronouns connected by and, use a plural verb.
She and her friends are at the fair.
2. When two or more singular nouns or pronouns are connected by or or nor, use a singular verb.
The book or the pen is in the drawer.
3. When a compound subject contains both a singular and a plural noun or pronoun joined by or or nor, the verb should agree with the part of the subject that is nearer the verb.
The boy or his friends run every day.
His friends or the boy runs every day.
4. Doesn't is a contraction of does not and should be used only with a singular subject. Don't is a contraction of do not and should be used only with a plural subject.
The exception to this rule appears in the case of the first person and second person pronouns I and you. With these pronouns, the contraction don't should be used.
He doesn't like it.
They don't like it.
5. Do not be misled by a phrase that comes between the subject and the verb. The verb agrees with the subject, not with a noun or pronoun in the phrase.
One of the boxes is open.
The people who listen to that music are few.
The team captain, as well as his players, is anxious.
The book, including all the chapters in the first section, is boring.
The woman with all the dogs walks down my street.
6. The words each, each one, either, neither, everyone, everybody, anybody, anyone, nobody, somebody, someone, and no one are singular and require a singular verb.
Each of these hot dogs is juicy.
Everybody knows Mr. Jones.
Either is correct.
7. Nouns such as civics, mathematics, dollars, measles, and news require singular verbs.
The news is on at six.
Note: the word dollars is a special case. When talking about an amount of money, it requires a singular verb, but when referring to the dollars themselves, a plural verb is required.
Five dollars is a lot of money.
Dollars are often used instead of rubles in Russia.
8. Nouns such as scissors, tweezers, trousers, and shears require plural verbs. (There are two parts to these things.)
These scissors are dull.
Those trousers are made of wool.
9. In sentences beginning with there is or there are, the subject follows the verb. Since there is not the subject, the verb agrees with what follows.
There are many questions.
There is a question.
10. Collective nouns are words that imply more than one person but that are considered singular and take a singular verb, such as: group, team, committee, class, and family.
In very few cases, the plural verb is used if the individuals in the group are thought of and specifically referred to.
The team runs during practice.
The committee decides how to proceed.
The family has a long history.
My family have never been able to agree.
11. Expressions such as with, together with, including, accompanied by, in addition to, or as well do not change the number of the subject. If the subject is singular, the verb is too.
The President, accompanied by his wife, is traveling to India.
All of the books, including yours, are in that box.
Homework due 12/03
Study your worksheet on Subject/Verb agreement
Study your WWW's
Write your WWW's 10X
Find definitions using your WWW's
Finish Type 5 Essays
Math:
Write a 2-page essay about some topics with which you have the most difficulty in math.
If you feel you do not have any difficulties in math, what do you like most about math this year?
SKIP LINES
Word Wall Words #11
Conceited: (adjective) having an excessively favorable opinion of one's abilities, appearance: being into one’s self
Knowledgeable: (adjective) intelligent, well-informed
Extensive: (adjective): broad, thorough, comprehensive, big
Suspenseful: (adjective): exciting, engaging, cliff-hanging
Tuesday, November 27, 2007
Homework due 11/28
Write sentences using your WWWs.
Math:
Please do your test corrections if you have not handed them in.
Finish your class work
Announcement:
We have two visitors tomorrow!
Monday, November 26, 2007
Word Wall Words #10
Antagonist (noun)
Protagonist (noun)
Compassion (noun)
For some reason, poor Ms. Simmons left her list at school, and she cannot remember the last word. Of course, you all are responsible enough to have it written in your packets already.
Love,
Ms. Simmons
Homework due Tuesday, November 27
Do your Test Corrections
Do your math worksheet on listing outcomes of dependent events
ELA:
Write your WWW 10X
Find definitions of the WWW's
Sunday, November 25, 2007
An aeriel picture of Middlebury College
Homework due on Monday, 11/26
Do your math packet
ELA:
Do your ELA packet
Announcements:
If you were absent, your packets are due on Friday.
THANK your parents!
Tuesday, November 20, 2007
Homework due tomorrow, Wednesday, 11/20
Math: Study for your math quiz which includes substitution and solving inequalities.
Social Studies:
Study for your quiz. Click here.
Other:
Bring 2 cans of food.
Bring food for our Thanksgiving celebration.
Monday, November 19, 2007
Word Wall Words #10 and definitions
Protagonist: The main character in a literary piece of work. Protagonist is a term used to refer to the figure or figures in literature whose intentions are the primary focus of a story. Classically protagonists are derived from good will, however, this does not always have to be true. Protagonists cannot exist in a story without opposition from a figure or figures called antagonist(s).
Homework due Tuesday, November 20
Study for your quiz. It will be on solving inequalities and substituting values for variable.
Do the homework entitled: Math Quiz. We will go over this in class.
ELA:
Study your word wall words.
Write an essay about your experience at Columbia University. If you did not go on the trip, you should write an essay about what you did instead of attend the trip.
WWW:
Protagonist
Antagonist
Sunday, November 18, 2007
TEAK Fellowship Information Session
Wednesday, November 28, 2007
6:30-8:00pm
The TEAK Fellowship Office
16 West 22nd Street, 3rd Floor
(between Fifth & Sixth Avenues)
New York, NY
Learn more about the TEAK fellowship at: http://www.teakfellowship.org/
Homework due on Monday
My wonderful Class of 2017,
I hope that you all enjoyed your trip to Columbia University on Friday! I had a lovely time and was so happy to see you all so happy there. I cannot wait until you all go to college!!!
All my love,
Ms. Simmons
Thursday, November 15, 2007
Homework due tomorrow, Friday, November 16
Study for your WWW quiz
Write an essay about the following topic: What do you think of college?
Math:
Do workbook pages 55 and 56
Annoucement:
Please wear your uniform to the trip. I am not bringing any students who do not have their uniform.
Homework due today, November 15
Do review worksheet
Study for quiz
ELA:
Study for WWW quiz
Write a paragraph using WWWs
Finish your Type 4 writing assignment
Announcements:
Bring your permission slip for our trip to Columbia University signed!
Tuesday, November 13, 2007
Homework due on Wednesday, 11/14
ELA:
Study for your WWW quiz this Friday before the trip
Write sentences using WWWs
Write WWWz 10X
Announcements: Bring money to donate to the Dominican Republic
Monday, November 12, 2007
Solving Inequalities
An inequality is used when we don't know exactly what an expression is equal to.
In order to solve an inequality, we have to combine like terms like you would if you were solving an equation.
For example, if you are asked to solve for x in the following equation: 5x + 3 = 13, you all know that you had to subtract 3 from both sides of the equation because our goal is to get x by itself and also because we know we have to do the inverse operation. In this case, the inverse of addition is subtraction.
After you subtracted 3 from both sides of the equation, you should have been left with 5x = 10. We have to get 5 from x because again, our goal is to get x by itself. Because we know that 5x is really 5 times x, we know that we have to do the inverse of multiplication to get x alone. So, we divide both sides by 5. Then, we are left with x = 10.
We use the same skills we use to solve equations to solve inequalities. We have to remember that our goal is to end up with a variable on one side of the inequality and a value on the other side.
Word Wall Words #9 and Definitions
Abruptly: (adverb) sudden or unexpected
Delinquent: (noun) a person who is guilty of a misdeed or offense; someone who breaks the law
Appeal: (verb) to be especially attractive, pleasing, interesting, or enjoyable. If something appeals to you, it is pleasing to you. For example, the author appeals to my senses because he writes with such descriptive language.
Appeal is a word we have seen before, but it seems that many of you have forgotten it.
Homework due tomorrow, Tuesday, November 13
Complete WWW quiz corrections
Write an 2-page essay about what frustrates you. Feel free to use your notes from our free writing exercise
Math:
Do your worksheet on solving inequalities
Do test corrections on the quiz you took on Friday
Announcements:
Bring canned goods or $2 to donate to the people in the Dominican Republic
Wednesday, November 7, 2007
Homework due tomorrow
In your workbook, do pages 53-56
ELA:
Bring your RAMPS paycheck signed by your parents
Study for your WWW quiz
Write a paragraph using your WWWs
Write a 2-page essay on the importance of community in a classroom
Bring $2 dollars and any canned goods you have for us to donate to DR
Tuesday, November 6, 2007
Helping others who need help

As some of you may already know, the Dominican Republic was greatly affected by Hurricane Noel. Authorities in the Dominican Republic confirmed 79 deaths and said at least 62,000 were left homeless by the storm. Dominican Republic is also suffering from severe flooding.
Imagine having a roof over your head one day and having no clothes, no bed, no toys, nowhere to call home the next day. Imagine not having clean drinking water or not being able to eat when you are hungry. Imagine walking around in dirty flood water with human waste floating around.
Because we are the Power Point Class, I think it is necessary that we do something to help the situation and the people in the Dominican Republic. So, if you all read this, please bring any cash donation that you can and canned food to class tomorrow.
We are also going to form a group to go around to other classes to collect canned goods and money.
Let's help others in need.
With love,
Ms. Simmons
Monday, November 5, 2007
Word Wall Words #8 and Definitions
bewilderment (noun): The condition of being confused or disoriented.
divert (verb): To distract: My attention was diverted by an argument between motorists.
reluctantly (adverb): unwillingly
exploit (verb): to use selfishly for one's own ends. For example, employers exploit their undocumented workers.
Homework due on Wednesday, 11/7
Do your two work sheets on solving equations
Do your test corrections for quiz translating verbal expression into equations quiz (7.A.1)
ELA:
Write your WWWs 10X
Find definitions for WWWs
Write sentences using your WWWs
Study for your WWWs
Do your Activity 4 for The Outsiders (Thanks, Jehiza!)
**If you forgot to bring in your summary on Earth and Sky Cakes (Type 3) or your Type 1 writing assignment, please bring it in on Wednesday!
Annoucements:
There is no school tomorrow. Enjoy your day off. I'll be coming to school, and I'll miss you all lots.
Friday, November 2, 2007
Homework for the weekend
ELA:
Finish your type 3 Writing Assignment. You are to write a summary of Earth and Sky Cakes. You must have at least ten sentences. You must have at least five adjective, adjective noun combinations, and you must put capital letters at the beginning of each sentence.
Study for your WWW quiz.
Annoucements:
Please find your power point class MOJO (good behavior) and bring it in on Monday.
Thursday, November 1, 2007
Homework due on Friday, 11/2
Study for your quiz on translating verbal expressions to algebraic expression and on rational and irrational number
Do your worksheet
ELA:
Study for your WWW quiz.
Write a 4-page summary of the first six chapters in The Outsiders
Announcements:
Bring $2 for a class celebration
Wednesday, October 31, 2007
Homework due tomorrow
No homework. Enjoy your trick-or-treating!
ELA:
Study your WWWs
Write a paragraph using your WWWs. Keep parts of speech in mind.
Tuesday, October 30, 2007
Homework due tomorrow
Workbook pages 45 and 46
ELA:
Write a 2-page essay about the worst or best Halloween experience you have had
Write sentences using WWWs
Announcements:
Get you progress reports signed
Monday, October 29, 2007
Homework due tomorrow/WWW quiz correction directions
Do your test corrections in the correct format (you can look through the blog, as I posted the information you need for preparing good test corrections)
ELA:
Write WWWs 10X and find definitions of the words
Do WWW quiz corrections:
Word Wall Word Test Correction Directions
1) Answer the same 6 reflection questions you have to answer to do math test/quiz corrections
2)Correct your errors in the fill in the blank section by telling me what you did wrong and how you found the correct answers
3) In the context clues section, re-answer the question and explain what clues you used to select your answer
4) In the making inferences question, elaborate your answers
5) In the parts of speech section, name the correct part of speech for each word and explain why you were confused (Please refer to the post I did on parts of speech to review if you need to)
Word Wall Words #6 and Definitions
Premonition: noun: a feeling of anticipation of or anxiety over a future event
Savage: noun: fierce, ferocious, or cruel; untamed
Survey: verb: to view in detail, esp. to inspect, examine, or appraise formally or officially in order to ascertain condition, value, etc
Hysteric: noun: a person who cannot control his or her outburst of emotion or fear
Opportunities for you: A Better Chance
A Better Chance is the preeminent resource for identifying, recruiting and developing leaders among young people of color in the United States.
Through a unique assessment model, A Better Chance refers academically talented students entering grades 6 through 11 to some of the nation's finest independent and public schools to be considered for placement and financial aid. Students who are successfully placed in one of our 300+ member schools become a part of the signature College Preparatory Schools Program, and receive access to expanded educational and leadership opportunities.
The College Preparatory Schools Program (CPSP) is an academic program that identifies, recruits, places, and supports students of color, in outstanding college preparatory middle and high schools nationally.
At A Better, Chance we recognize that students come from different backgrounds and educational opportunities so each application is evaluated on its own merit. Generally, we select students who:
1) Consistently perform at or above grade level in math and English
2) Have an overall academic average of a B+ or better
3) Are ranked in the top 10 percent of the class
Students are required to take standardized tests. There are no score cut-offs but test scores are used to assess academic strength along with school transcripts, extracurricular activities and personal qualities. Selected applications are sent to our member schools, but it is the admission committees of each member school that make the final admission decisions.
Prospective applicants should get started early; late applications are not encouraged as it severly limits opportunities for placements. Further, our application process begins one year prior to enrolling. For example, if a student is currently in the 8th grade, s/he would be applying for the 9th grade.
For more information: click here: http://www.abetterchance.org/abetterchance.aspx?pgID=866
Opportunities for you: Prep for Prep
Any 7th grader of Black and/ or Latino descent group background who has obtained the scores specified below is eligible to apply for admission to PREP 9. The eligibility criteria to apply to the PREP 9 program are as follows:
Student must have a scaled score of at least 700 on the CTB (or any standardized) Reading test administered during the 2006-2007 school year (6th grade) or student must have a grade point average of 90% and above in major subject areas.
Please be prepared to provide us with a copy of your child’s 2006-2007 Reading scores or a copy of 2006-2007 report card.
Download one of the forms below to learn more about the PREP 9 Admissions process:
Admissions Information (English)
Admissions Information (Spanish)
For more information, please email prep9_admissions@prepforprep.org.
Opportunities for you: TEAK Fellowship
TEAK's application process begins in October each year. Through a comprehensive six-month process, applicants participate in several rounds of screening that include a financial assessment, diagnostic tests, a written application, and interviews. TEAK's five-year Fellowships are awarded based on both academic merit and financial need.
Qualified candidates MUST:
- Be enrolled in the SEVENTH grade at the time of their application
- Attend a PUBLIC or PAROCHIAL school in one of the five boroughs of NYC
- Earn 3s & 4s or 90% AND ABOVE in all grades and on tests
- Come from families WITH FINANCIAL NEED
- Provide proof of academic merit and income
- Be citizens or permanent residents of the United States
Each spring, TEAK accepts 25 students as Fellows. They begin attending the Spring Intensive in May, participate in the Summer Institute following their seventh and eighth grade school years, and begin the High School Placement process by attending after-school and Saturday activities during their eighth grade school year. Fellows enter the Post-Placement program during high school and continue their Fellowship until they go to college.
Saturday, October 27, 2007
Homework due on Monday, 10/29
Those of you who owe me ELA work have to do a 2-page essay for each assignment you missed. That is, if you owe me 10 assignments, then, you must do 10 2-page essays for me. I will be looking at content and grammar. If you put no care of effort into your work, I will be able to see that and will grade accordingly.
You could write about any topic. Some things that you could write about are:
What do you think of 7th grade so far?
What do you like doing on the weekends?
What do you like about our class book, The Outsiders? Why?
Do you feel that you have a voice in society? Why or why not?
What about your neighborhood bothers you? Why?
What makes you proud to be who you are? Why?
What makes you proud to be in the Power Point Class? Why?
What do you want in a teacher? Why?
If you could change anything about your school, what would you change? Why?
If your heart is telling you that you want to write a 20-page story instead of 10 2-page essays, that is fine too. I will not be lenient when grading these, as you should have done your work in the first place.
I am allowing you all to make up work, despite your irresponsibility, because I want you all to go to the high schools of your dreams. Next marking period, I will not allow you to make up any work. You have to learn to be on point and to be responsible. You all are mature and old enough by now.
Love,
Ms. Simmons
Thursday, October 25, 2007
Do your math worksheet
Read your notes on rational and irrational numbers. Know what repeating and a non-repeating decimals are and what terminating and non-terminating decimals are.
ELA:
Study for your WWWs quiz
Study your notes on apostrophes
Study your notes on parts of speech (notes are on this blog!)
Write a 2-page essay on the importance of paying attention in class
Wednesday, October 24, 2007
Repeating/Non-repeating decimals and Terminating and Non-terminating decimals
The word rational refers to something reasonable, understandable, within reason. In short rational numbers are whole numbers, fractions, and decimals - the numbers we CAN understand and that we use in our daily lives.
In mathematical terms a number is rational if you can write it in a form a/b where a and b are integers, b not zero. Clearly all fractions are of that form. Terminating decimal numbers can easily be written in that form: for example 0.67 is 67/100, 3.40938 = 340938/100000 etc.
Terminates means to end. So, if you decimal ends, it is a rational number. For example, .46 is a rational number because it is terminating.
Irrational Numbers:
Rational numbers are contrasted with irrational numbers - such like Pi and square roots of non-perfect squares of numbers. In a sense you can't really understand the irrational numbers, because the name irrational itself means NOT rational, NOT reasonable, NOT understandable, NOT within reasoning powers.
Repeating decimals:
A repeating decimal, also called a recurring decimal, is a number whose decimal representation eventually becomes periodic (i.e., the same sequence of digits repeats indefinitely).
.333333333333... is a repeating decimal because 3 repeats. The (...) tells you that 3 goes on and on and that the decimal is non-terminating, which I will go over shortly. (Look below)
Non-repeating decimals:
Non-repeating decimals are decimals that do not have a repeating pattern. For example, the value for Pi is a non-repeating decimal. Its value is: 3.14159265.... You cannot predict any type of pattern for pi. It's irrational.
Terminating decimals:
Terminating decimals are decimals are decimals that END; they do not go on and on and on and on. 6.5 and 0.0000034 are examples of terminating decimals. They stop. They do not go on and on.
Non-terminating decimals:
Non-terminating decimals do not end. They go on forever. The (...) or the line over your decimals indicated that your decimals are non-terminating.
For example, 6.33333333333.... is non-terminating.
Now, how do we figure out what decimals are rational or irrational?
Irrational decimals will be BOTH non-terminating and non-repeating decimals. All other types of decimals will be rational. That is, if your decimal is not BOTH non-terminating and non-repeating, then, it is not irrational.
For example, if a number is non-terminating, but it is repeating, then it is rational. .3333... is repeating and non-terminating. It is rational because it does not BOTH non-repeating and non-terminating. It satisfies ONLY one of the rules.
Homework due tomorrow
Do worksheet on rational and irrational fractions.
ELA:
Study for your WWW quiz
Study the usage of apostrophes
Study your parts of speech (there is information on the blog about parts of speech)
Write a paragraph using your WWW's
Write a 2-page essay about your favorite character in The Outsiders so far. Please tell me why you selected the character you selected.
Tuesday, October 23, 2007
Homework due tomorrow
Do pages 5 and 6 in your text book
Do your worksheet
ELA:
Do The Outsiders worksheet on Chapter three. Please write reflective responses.
Study for your WWW quiz.
Write sentences for your WWWs.
Word Wall Words #5 and Definitions
Sullenly: adverb: showing irritation or ill humor by a gloomy silence or reserve, ill-humored.
Evade: verb: to avoid or escape by speed, cleverness, trickery
Fiend: noun: a person or thing that causes mischief or annoyance; an evil person
Indignant: adjective: feeling, characterized by, or expressing strong displeasure at something considered unjust, offensive, insulting, or base
Monday, October 22, 2007
Rational and Irrational Numbers
Rational Numbers
A rational number is a number that can be written as a ratio. That means it can be written as a fraction, in which both the numerator (the number on top) and the denominator (the number on the bottom) are whole numbers.
- The number 8 is a rational number because it can be written as the fraction 8/1.
- Likewise, 3/4 is a rational number because it can be written as a fraction.
- Even a big, clunky fraction like 7,324,908/56,003,492 is rational, simply because it can be written as a fraction.
 |
Every whole number is a rational number, because any whole number can be written as a fraction. For example, 4 can be written as 4/1, 65 can be written as 65/1, and 3,867 can be written as 3,867/1.
Irrational Numbers
All numbers that are not rational are considered irrational. An irrational number can be written as a decimal, but not as a fraction.
An irrational number has endless non-repeating digits to the right of the decimal point. Here are some irrational numbers:
π = 3.141592…
= 1.414213…
Although irrational numbers are not often used in daily life, they do exist on the number line. In fact, between 0 and 1 on the number line, there are an infinite number of irrational numbers!
Parts of Speech
For more information besides the many handouts I gave you in class, this site is very helpful. Click here.
Briefly, the noun is a person, place, thing, or idea.
The adjective describes a noun.
The adverb indicates manner, time, place, cause, or degree and answers questions such as "how," "when," "where," "how much". Adverbs generally end in "ly."
The preposition usually indicates the temporal, spatial or logical relationship of its object to the rest of the sentence.
The interjection is a word added to a sentence to convey emotion. It is not grammatically related to any other part of the sentence.
You can use a conjunction to link words, phrases, and clauses, as in the following example:
- I ate the pizza and the pasta.
- Call the movers when you are ready.
he verb is perhaps the most important part of the sentence.
A verb or compound verb asserts something about the subject of the sentence and express actions, events, or states of being.
Word Wall Words #5
Sullenly (adverb)
fiend (noun)
Indignant (adjective)
Evade (verb)
Homework due tomorrow
Do your test corrections for your Unit 2 Test. If you did not get a 100 percent, then, you must do test corrections even if you are satisfied with you grade. There is always room for improvement.
Do workbook pages I put on the board (I'm making sure that you write down the homework in your agenda when I tell you to do so. Thus, you have the pages if you followed directions in class today.)
ELA:
Find the definition of your WWWs
Write the words out 10X each
Study your WWWs just in case you receive a pop quiz.
Do your Review: Parts of Speech packet. (We will go over it in class. I have considered counting it as a quiz card. Take your time.)
Wednesday, October 17, 2007
Homework due tomorrow
**Do your worksheet on scientific notation
**Study for your quiz.
ELA:
**Study for WWW quiz
**Write a paragraph using the WWWs
**In your pronoun packet, read page 118. Read page 119 and do Exercises 1 and 2 on 119 and 120.
**Make 3 predictions about what you think will happen in The Outsiders.
Tuesday, October 16, 2007
Word Wall Words #5 and Definitions
Apprehensive (adjective): uneasy or fearful about something that might happen.
Aloofness (noun): at a distance, esp. in feeling or interest; apart.
Defiance (noun): a daring or bold resistance to authority or to any opposing force.
Contemptuously (adverb): showing or expressing contempt or disdain; scornful.
Scientific Notation Lesson with big numbers
Scientists have developed a shorter method to express very large numbers. This method is called scientific notation. Scientific Notation is based on powers of the base number 10.
The notation is based on powers of base number 10. The general format looks something like this:
N X 10x where N= number greater than or equal to 1 but less than 10 and x=exponent of base 10.
Placing numbers in exponential notation has several advantages.
For very large numbers and extrememly small ones, these numbers can be placed in scientific notation in order to express them in a more concise form.
In addition, numbers placed in this notation can be used in a computation with far greater ease. This last advantage was more practical before the advent of calculators and their abundance.
In scientific fields, scientific notation is still used.
Let's first discuss how we will express a number greater than 10 in such notational form.
Numbers Greater Than 10
We first want to locate the decimal and move it either right or left so that there are only one non-zero digit to its left.
The resulting placement of the decimal will produce the N part of the standard scientific notational expression.
Count the number of places that you had to move the decimal, and that would be your x, exponent.
If it is to the left as it will be for numbers greater than 10, that number of positions will equal x, the exponent, in the general expression above.
As an example, how do we place the number 2340000 in standard scientific notation?
Position the decimal so that there is only one non-zero digit to its left. In this case we end up with 2.34. We know that 2.34 has to be less than 10 and has to be greater than or equal to 1.
Count the number of positions we had to move the decimal to the left and that will be the exponent, x.
So we have: 2.34 X 106 in scientific notation.
That is how we convert from standard form to scientific notation.
Now, how do we go from scientific notation to standard form:
(1) Move decimal point to right the same amount of times your exponent tells you to.
For example, if your base ten exponential has an exponent of 5, you have to move the decimal point to the right 5 times.
That is, 5.67 x 105 is: 567000.
Good luck!! You all did a great job in class today.
Homework due tomorrow, Wednesday, 10/17
Do your worksheet on scientific notation with big numbers
ELA:
Write sentences using your WWWs
Write an 2-page essay about what you think about 7th grade so far. SKIP LINES.
Do your worksheet on conjunctions.
Saturday, October 13, 2007
Homework due on Monday
**Write a 4-page creative story about anything you want. Your story must engage the reader. Remember to use sensory details! SKIP LINES.
Math:
**In your workbook, do pages 27-30.
**Work on your test corrections!!!
Tuesday, October 9, 2007
Word Wall Words #4
Love,
Ms. Simmons
Math Worksheet #3
1. Write the following numbers in exponential form.
5 × 5 × 5 × 5 × 5 × 5 × 5
9 × 9 × 9
7 × 7 × 7 × 10 × 8 × 8
3 × 7 ×7 × 7 × 7 × 3 × 3
1 × 2 × 3 × 3 × 3
2. Write the following numbers as repeated multiplication.
32
43
34
810
3. Evaluate the following expressions:
33 + 32 – (4 + 8)
6 – 9 × (-4)2
31 + 40 + 52
4. Write the squares of the following numbers:
32 = _______
142 = _______
92 = _______
152 = _______
5. Write the square roots of the following perfect squares:
√25 = _______ √36 = _______ √100 = _______ √169 = _______
6. Using the number lines below, show approximately where the value of the square root of the included number is. Be sure to show the whole number before and after the square root.
Show the square root of 11, and the whole numbers that √11 lies between.
Show the square root of 175, and the whole numbers that √175 lies between.
Math Worksheet #2
1. Using the number lines below, give the two whole numbers that each of the following square roots lie between:
√2
√6
√10
√12
√17
√21
√38
√45
√29
2. Without using a number line or a calculator, find the two whole numbers that each of the square roots below lie between:
√80
√110
√200
√175
√215
√115
√99
√70
√150
3. Using a calculator, find the square roots of the following numbers. See if they match what you did in number 2 on the other side of this worksheet.
√80 =
√110 =
√200 =
√175 =
√215 =
√115 =
√99 =
√70 =
√150 =
4. Circle the perfect squares. Then, without using a calculator, give their square root.
169
100
110
60
49
225
5
16
2
5. Write the following numbers in exponential form:
5 × 5 × 5 × 5 × 5 × 5 × 5
6 × 6 × 6
7 × 7 × 7 × 7 × 8 × 8
6. Write the following numbers as repeated multiplication:
72
85
99
52 × 35
Math Worksheet #1
Remember: When multiplying exponentials, there are two laws that can help you simplify the expression.
1st Multiplication Law: If the exponentials have the same base, add the powers.
2nd Multiplication Law: If the exponentials have the same power, multiply the bases.
Use the above laws to simplify the following problems.
1. 123 × 23 = ____________
2. 46 × 36 = ____________
3. 55 × 53 = ____________
4. 254 × 44 = ____________
5. 39 × 339 = ____________
6. 1012 × 104 = ____________
7. 75 × 35 = ____________
8. 246 × 36 = ____________
Problem number 3 follows the 1st law for multiplication of exponentials (bases are the same). Write a problem that follows the 2nd law for multiplication of exponentials and simplify it.
______________________________________________________________________________
______________________________________________________________________________
______________________________________________________________________________
______________________________________________________________________________
Multiplication Laws
Base: The number used as a factor for repeated multiplication (the big number on the bottom)
Power: The number of times the factor is being multiplied, a.k.a. exponent (the number up top)
Simplify: The change to a more simple form (not the same as evaluate or solve!!)
There are laws for simplifying the *multiplication* of exponentials:
1st Multiplication Law: If the exponentials have the same base, the powers can be added: 52 × 53 = 52+3 = 55.
It will be very important for students to see this in proof form, to help them visualize it: 52 × 53 = (5 × 5) × (5 × 5 × 5) = 5 × 5 × 5 × 5 × 5
2nd Multiplication Law: If the exponentials have the same powers, multiply the bases and keep the power: 53 × 63 = (5 × 6)3 = 303
Homework due tomorrow
**3 math worksheets (I will post them online for those of you who were absent)
ELA:
**Write the WWWs ten times each
**Write sentences using the WWWs. Make sure you show me that you know the meaning of the words.
Sunday, October 7, 2007
If you want to get ahead....
Word Wall Words #4
Conclude: (verb) to determine by reasoning; deduce; infer:
Ornery (pg. 39): (adjective) stubborn, having an unpleasant personality
Vaguely (pg. 33): (adverb) not clearly or explicitly stated or expressed
Rebellious (pg. 34): (adjective) defying or resisting some established authority, government, or tradition; insubordinate; inclined to rebel.
Gallant (pg. 37): (adjective) brave, spirited, noble-minded, or chivalrous.
How to do good test corrections?
What’s up with test corrections?
For every test that you take in this class, you are required to do test corrections even if you are satisfied with your grade. The point of test corrections is to give you the opportunity to improve and to demonstrate your understanding of the material.
When are test corrections due?
Test corrections are due a week after your receive your test. That is, if I give you back your test on Tuesday, you must return your test corrections to me by the following Tuesday. Since a week is sufficient time to work on your test correction, any late test corrections will result in a zero.
How to do a good test correction?
1. DO A TEST REFLECTION
On a separate piece of loose-leaf paper (not in your notebook), answer the following questions in complete sentences (so I can understand what you are trying to tell me!).
1. What grade did you get on your test?
2. What grade do you think you deserve (based on how much you learned from this unit)?
3. How much studying did you do for this test? Please describe HOW you prepared for this test.
4. Do you think your studying was effective? Why or why not?
5. Do you think you really UNDERSTAND this material?
2. CORRECT THE QUESTIONS YOU MISSED ON THE TEST ON A SEPARATE PIECE OF PAPER FROM YOUR REFLECTIONS
For EVERY SINGLE QUESTION you missed or lost ANY points on, do ALL of the following:
a. Write out the complete correct answer. (If you missed a multiple-choice question, you must write out an entire complete sentence, not just the letter of the answer. This does NOT mean you have to write out the entire question, just put the question into a complete sentence). You also must SHOW YOUR WORK.
b. You must explain how you came up with the correct answer.
b. Where did you find the correct answer? (This could be your notebook, the textbook, your brilliant teacher, etc)
3. ANSWER THIS LAST QUESTION
6. What (if anything) will you do differently next time while preparing for a test in this class?
4. STAPLE ALL THE PAGES TOGETHER, ATTACH YOUR TEST TO THE BACK, AND TURN THE WHOLE THING IN ON TIME!!!
How much are test corrections worth?
Test corrections are worth a quiz grade. If you do not complete your test corrections, you will get a zero. If your test corrections are late, you will receive a zero. If you received a perfect score on your initial test, then, you get an automatic 100 on the test correction!
Due on Tuesday, October 9
Because of the rapid dismissal, I was unable to give you the homework that I had planned for you. Don't worry. I know how excited you all are for homework. Thus, I will make sure to give you lots of homework when you get back. :)
Enjoy your day off. See you Tuesday.
Wednesday, October 3, 2007
Squares and Square Roots
How to Square A Number
To square a number, just multiply it by itself ...
Example: What is 3 squared?
| 3 Squared | = | 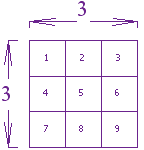 | = | 3 × 3 | = | 9 |
Note: we write down "3 Squared" as 32
(the little "2" means the number appears twice in multiplying)
Some More Squares
| 4 Squared | = | 42 | = | 4 × 4 | = | 16 |
| 5 Squared | = | 52 | = | 5 × 5 | = | 25 |
| 6 Squared | = | 62 | = | 6 × 6 | = | 36 |
Square Root
A square root goes the other direction:
3 squared is 9, so the square root of 9 is 3
| 3 |  | 9 |
The square root of a number is ...
... that special value that when multiplied by itself gives the original number.
The square root of 9 is ...
... 3, because when 3 is multiplied by itself you get 9.
 | Note: When you see "root" think "I know the tree, but what is the root that produced it?" In this case the tree is "9", and the root is "3". |
Here are some more squares and square roots:
 | ||
| 4 | 16 | |
| 5 | 25 | |
| 6 | 36 | |
Example: What is the square root of 25?
Well, we just happen to know that 25 = 5 × 5, so if you multiply 5 by itself (5 × 5) you will get 25.
So the answer is 5
The Square Root Symbol
| This is the special symbol that means "square root", it is sort of like a tick, and actually started hundreds of years ago as a dot with a flick upwards. It is called the radical, and always makes math look important! |
You can use it like this: ![]() (you would say "the square root of 9 equals 3")
(you would say "the square root of 9 equals 3")
More Advanced Topics Follow
You Can Also Square Negative Numbers
Have a look at this:
| If you square 5 you get 25: | 5 × 5 = 25 | |
| But you could also square -5 to get 25: | -5 × -5 = 25 | |
| (because a negative times a negative gives a positive) |
So the square root of 25 can be 5 or -5
There can be a positive or negative answer to a square root!
But when people talk about "the" square root they usually mean just the positive one.
And when you use the radical symbol √ it always means just the positive one.
Example: √36 = 6 (not -6)
Perfect Squares
The perfect squares are the squares of the whole numbers:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | etc | |
| Perfect Squares: | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 | 225 | ... |
It is easy to work out the square root of a perfect square, but it is really hard to work out other square roots.
Example: what is the square root of 10?
Well, 3 × 3 = 9 and 4 × 4 = 16, so we can guess the answer is between 3 and 4.
- Let's try 3.5: 3.5 × 3.5 = 12.25
- Let's try 3.2: 3.2 × 3.2 = 10.24
- Let's try 3.1: 3.1 × 3.1 = 9.61
Very slow ... at this point, I get out my calculator and it says:
3.1622776601683793319988935444327
... but the digits just go on and on, without any pattern. So even the calculator's answer is only an approximation !
(Further reading: these kind of numbers are called surds which are a special type of irrational number)
A Special Method for Calculating a Square Root
There are many ways to calculate a square root, but my favorite method is an easy one which gets more and more accurate depending on how many times you use it:
a) start with a guess (let's guess 4 is the square root of 10)
b) divide by the guess (10/4 = 2.5)
c) add that to the guess (2.5+4=6.5)
d) then divide that result by 2, in other words halve it. (6.5/2 = 3.25)
e) now, set that as the new guess, and start at b) again
... so, our first attempt got us from 4 to 3.25
Going again (b to e) gets us: 3.163
Going again (b to e) gets us: 3.1623
And so, after 3 times around the answer is 3.1623, which is pretty good, because:
3.1623 x 3.1623 = 10.00014
This is fun to try - why not use it to try calculating the square root of 2?Homework due tomorrow
In your workbook, do pages 79 and 80 on square roots.
ELA:
Write a paragraph using your WWW words.
Write a 2-page story about the picture we discussed today. SKIP LINES.
Tuesday, October 2, 2007
Homework due tomorrow
ELA: Write WWW sentences. Make sure your sentences show me that you understand the meanings of the words.
Word Wall Words #3 and Definitions
Roguishly (pg. 22): playfully mischievous (causing annoyance, harm, or trouble)
Incredulous (pg. 24): unbelievable, skeptical
Nonchalantly (pg. 25): coolly unconcerned, indifferent, or unexcited; casual
Feud (pg. 29): a quarrel, fight, or disagreement
Monday, October 1, 2007
Homework due tomorrow
Do your worksheet on exponents
ELA:
Find the definitions of your word wall words.
Write your word wall words 10X.
Study your word wall words.
Announcements:
It seems that we will be taking our exams tomorrow. Make sure you get plenty of rest.
Thursday, September 27, 2007
Answers to the Math HW
Explanation:
These are a few of the possible answers for number 1. We know that an integer is a counting number that is a whole number. So, in order to answer this question, you need to know what an integer is and you have to know what a sum means. The sum is the answer you get when you add numbers together.
2) It is possible that -5 is larger than -10 even though the absolute value of -10 is larger than that of -5 because -5 is closer to zero and closer to positive numbers of the number line.
From left to right:
3) -40
4) -2
5) 0
6) 108
7) 3
8) 1
9) -14
10) -27
LCM of 4 and 7 is 28.
GCF of 12 and 18 is 6.
Prime factorization 0f 54:
54
2 x 27
9 x 3
3 x 3
= 2 x 3 x 3 x 3
Solve the following proportion:
x = 49
Homework due Friday, September 28
**Your test corrections for your second quiz is due. Everyone must do it even if you are happy with your grade. There is a certain format for doing your corrections. Please make sure to follow the format or you will not receive full credit for the test corrections.
**Study for your unit test. Look through the blog to read through the lessons I posted.
ELA:
**Study for your WWW quiz.
**Do the sheet on predictions that I handed out at the end of class. You are supposed to make predictions about what you think will happen in The Outsiders based on the first chapter. You have to back up your answer from what we read in class today. Hopefully, you were paying attention.
Announcements:
**If you did not bring your lunch form, please bring them tomorrow.
**If you did not bring your blue contact card, bring tomorrow.
Wednesday, September 26, 2007
Homework due Thursday, September 27
**Finish you worksheet from class on order of operations.
**Do your homework sheet on order of operations.
ELA:
**Write a paragraph using your word wall words. Make sure to show me that you know the meanings of the words.
**Study for your WWW quiz.
Other annoucements:
**Remember to bring your lunch forms.
**Sleep well. Tomorrow, we will be taking a standardized test. I am positive you all will do very well!
Tuesday, September 25, 2007
What is mapping?
Mapping is how we lay out the ideas visually to find connections and to branch out and make new ideas and connections. Eventually mapping will lead you to a list of ideas and a sequence to use them in.
1. How to use mapping to generate ideas:
Write the topic in the middle of the page. Draw branches out from that topic and write keywords or phrases that you associate with that topic. Draw more branches out from each of those keywords (sub-topics) to develop each of those ideas. Look, then, at which of the sub-topics go together and if any of the extended ideas can link to each other. Draw branches and lines between the ideas that could work together. Decide, then, if you would like to regroup your ideas.
Write the topic in the middle of the page again and go through the first steps again with the new groupings.
Do this as many times as you like until you have clear responses and ideas that you can now form into the parts of an essay. With the bubbles and branches you can see how the ideas work, how they interrelate and how they work together as a whole.
Before you write your paper it is a good idea to choose what order your ideas will be written in. This will ensure that you answer the whole question, remember all the parts, and that your answer can have a logical flow. An essay is a complicated answer and it is important that all of the parts of the essay (introduction/body paragraphs/conclusion) work together in a way that is easy to read, logical, and that builds together to the conclusion. This can't happen if the parts are jumbled or random.
It is important to work out which idea should go first, which ideas are prerequisite to other ideas, etc. What is your most dramatic idea? Which ideas work together to form another, bigger idea? With all of these elements going on, it is important to write down a list of the order you will use. To decide on that order you may have to work out what kind of structure you need first or, if you already know that, you may be able to proceed straight to the plan (also known as an outline.)
Solving Proportions
 . A statement such as this that one ratio is equal to another is called a proportion.
. A statement such as this that one ratio is equal to another is called a proportion.

Proportional reasoning involves the ability to compare and produce equal ratios. A common use of proportions occurs when making or using maps and scale models.
There are several ways to solve a proportion. One is related to how you find equivalent fractions. To find equivalent fractions, you multiply or divide the numerator and denominator by the same number. Thus, to solve  , note that the numerator (2) was multiplied by 3 in order to get 6. Then do the same to the denominator (3) to get n=9. This works well when the numerator and denominator of one fraction are multiples of the other fraction, but it is more difficult to do when they are not, as in the case of
, note that the numerator (2) was multiplied by 3 in order to get 6. Then do the same to the denominator (3) to get n=9. This works well when the numerator and denominator of one fraction are multiples of the other fraction, but it is more difficult to do when they are not, as in the case of  . In this case we multiply both sides of the equation by 8n as shown below:
. In this case we multiply both sides of the equation by 8n as shown below:
 | |
 | (multiplying both sides by 8n) |
 | (divide out the common factors) |
 | (divide both sides by 6) |
 | (simplify) |
 . This cross product property only works when solving a proportion. It does not apply when doing operations with fractions, such as multiplying or dividing fractions. Using this idea of cross multiplying inappropriately is a common problem students have. The reason it works is because you are really multiplying both sides of an equation by the product of the two denominators.
. This cross product property only works when solving a proportion. It does not apply when doing operations with fractions, such as multiplying or dividing fractions. Using this idea of cross multiplying inappropriately is a common problem students have. The reason it works is because you are really multiplying both sides of an equation by the product of the two denominators.Source: http://www.eduplace.com/math/mathsteps/6/a/index.html
Word Wall Words
Suffocate (5): (verb): to strangle
Opponent (11): (noun) a person who is on an opposing side in a game, contest, controversy, or the like
Perspiration (4): (noun) the act of sweating
Cuss (5): (verb) to use profanity; curse; swear
Homework due tomorrow
**Do your worksheet on solving proportions
**Finish your test corrections for your first quiz
**Your second set of test corrections is due on Friday
NOTE: If you do not hand in your test corrections tomorrow, you get an automatic zero. I gave you a week to get them done. NO EXCUSES, kiddos.
ELA:
**Write sentences for your word wall words
**Study for your word wall word quiz
**Do a map for a topic of your choice.
EXTRA CREDIT: Write a 2-page essay based on your map. SKIP LINES.
Monday, September 24, 2007
Homework due on Tuesday, 9/25
**In your workbooks, please do pages 9-16. I will be checking them tomorrow. If there is something you do not understand, please let me know. I would prefer if you write a letter to let me know in writing.
**Please review adding and subtracting integers lesson on the blog.
ELA:
**Find the definitions of your word wall words and write the words 10 times each. I would like your work to be neat.
**Do The Outsiders Anticipatory Guide. We will discuss it briefly in class tomorrow.
RAMPS:
**Get your RAMPS paycheck signed.
Sunday, September 23, 2007
Homework due on Monday, 9/24
Do your math worksheet on multiplying and dividing integers
Go over your notes on adding and subtracting integers
ELA:
Write a 4-page essay on what you did for your summer vacation. SKIP LINES.
Make sure you come to school on time and ready to learn. We are all trying to get 45 RAMPS points or more so that we could have our class celebration.
Love,
Ms. Simmons
Thursday, September 20, 2007
Multiplying and Dividing Integers
When you multiply two integers with the same signs, the result is always positive. Just multiply the absolute values and make the answer positive.
Positive x positive = positive
Negative x negative = positive
When you multiply two integers with different signs, the result is always negative. Just multiply the absolute values and make the answer negative.
Positive x negative = negative
Negative x positive = negative
Dividing Integers:
When you divide two integers with the same sign, the result is always positive. Just divide the absolute values and make the answer positive.
Positive ÷ positive = positive
Negative ÷ negative = positive
When you divide two integers with different signs, the result is always negative. Just divide the absolute values and make the answer negative. Just multiply the absolute values and make the answer negative.
Positive x negative = negative
Negative x positive = negative
Word Wall Words and Definitions
Reckon: to esteem or consider; regard as
Asset: a useful and desirable thing or quality
Disgrace: a person, act, or thing that causes shame, reproach, or dishonor or is dishonorable or shameful.
Unfathomable: Difficult or impossible to understand; incomprehensible
What makes a proficient reader?
* see yourselves as readers.
* make sense of text.
* use what you know.
* understand how stories work.
* read to learn.
* monitor and organize ideas and information.
* think critically about books.
The main way to become a better readers is to:
* read
* read
* read
* read
* read
* read
* read
* ..and read some more!!
Why do we read?
Reading involves an interaction between a specific type of text or written material and a reader who has a purpose for reading that is related to the type of text and the context of the reading situation.
The three purposes for reading are:
Reading for literary purpose
Reading to gain information
Reading to perform a task
Reading for literary purpose:
Reading for literary experience involves reading literary text to explore the human condition, to relate narrative events with personal experience, and to consider the interplay in the selection among emotions, events, and possibilities.
Reading to gain information:
Reading to gain information involves reading informative passages in order to obtain some general or specific information. This often requires a more practical approach to reading that requires the use of certain reading/thinking strategies different from those used for other purposes. In addition, reading to gain information often involves reading and interpreting aids such as charts, graphs, maps, and tables that provide data.
Reading to perform a task:
Reading to perform a task involves reading various types of materials for the purpose of applying the information or directions in completing a specific task. The reader’s purpose for gaining meaning extends beyond understanding the text to include the accomplishment of a certain activity.
Homework
**Study for your quiz on adding, subtracting, multiplying, and dividing integers.
ELA:
**Study for your word wall word quiz.
**Study your reading notes on what makes a proficient reader and what are the purposes of reading.
**Smile because Ms. Simmons loves you, and get a good night's rest!
Wednesday, September 19, 2007
Adding and Subtracting Integers
Whole numbers are the counting numbers including 0. For example, 1, 2, 3, and 108 are wholes numbers. 3.5, 4.009, and Pi are not whole numbers.
Whole numbers greater than zero are called positive integers.
Whole number less than zero are called negative integers.
Use the number line for adding and subtracting integers:
• Add a positive integer by moving to the right on the number line
• Add a negative integer by moving to the left on the number line
• Subtract an integer by adding its opposite
We can use the number line as a model to help us visualize adding and subtracting of signed integers. Just think of addition and subtraction as directions on the number line. There are also several rules and properties that define how to perform these basic operations.
**To add integers having the same sign, keep the same sign and add the absolute value of each number.
**To add integers with different signs, keep the sign of the number with the largest absolute value and subtract the smallest absolute value from the largest.
**Subtract an integer by adding its opposite.
IN-DEPTH:
Here's how to add two positive integers:
4 + 7 = ?
If you start at positive four on the number line and move seven units to the right, you end up at positive eleven. Also, these integers have the same sign, so you can just keep the sign and add their absolute values, to get the same answer, positive eleven.
Here's how to add two negative integers:
-4 + (-8) = ?
If you start at negative four on the number line and move eight units to the left, you end up at negative twelve. Also, these integers have the same sign, so you can just keep the negative sign and add their absolute values, to get the same answer, negative twelve.
Here's how to add a positive integer to a negative integer:
-3 + 6 = ?
If you start at negative three on the real number line and move six units to the right, you end up at positive three. Also, these integers have different signs, so keep the sign from the integer having the greatest absolute value and subtract the smallest absolute value from the largest.
Subtract three from six and keep the positive sign, again giving positive three.
Here's how to add a negative integer to a positive integer:
5 + (-8) = ?
If you start at positive five on the real number line and move eight units to the left, you end up at negative three. Also, these integers have different signs, so keep the sign from the integer having the greatest absolute value and subtract the smallest absolute value from the largest, or subtract five from eight and keep the negative sign, again giving negative three.
To subtract a number, add its opposite:
5 - 8 = ?
Because they give the same result, you can see that subtracting eight from five is equivalent to adding negative eight to positive five. The answer is - 3.
To subtract a number, add its opposite:
-3 - (-6) = ?
Because they give the same result, you can see that subtracting negative six from negative three is equivalent to adding positive six to negative three. The answer is 3.



